The Force of Friction on a Banked Surface calculator computes the minimum force of friction to keep a vehicle on a slope based on the mass and velocity of the car, angle of banked surface, and the radius of the curve.
INSTRUCTIONS: Choose units and enter the following:
- (m) Mass of the Vehicle
- (Φ) Angle of the the Banked Surface
- (v) Velocity of the Vehicle
- (r) Radius of the Curve
Frictional Force (Ff): The force is returned in newtons. However, this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
The Force of Friction (banked surface) equation calculates the minimum force of friction (`F_f`) required to keep a car from sliding outward in a turn on a banked surface. The force model depicted in the Figure 1 shows a car on a banked curve. The force of gravity pulls the vehicle down the incline. The centripetal force of the car's acceleration through the curve pulls the car outward and upward on the curve. The frictional force between the tires and the banked surface creates a countering resisting force acting against the gravitational and centripetal forces.
Definition
The force of friction, `F_f`, required to keep the car on the banked turn is:
`F_f = (m*g * sin(phi) - m*v^2 /r * cos(phi))`
with the following parameters
| Parameter | Value |
|---|---|
| m - the mass of the car | - |
| g - Earth-surface gravitational acceleration | 9.80665 m/s2 |
| `phi` - the angle of the banked surface | - |
| v - the velocity of the vehicle | - |
| r - the radius of the curve | - |
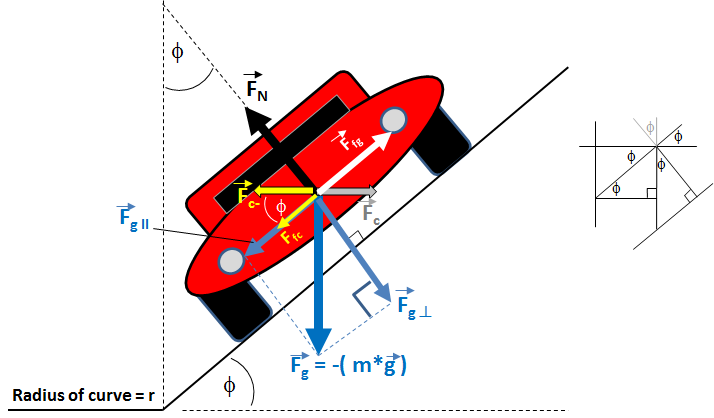Figure 1
Derivation
Figure 1 depicts the back end of a car turning to the left. (`vecF_g`) is the weight of the car due to the force of gravity pulling it downward. The perpendicular component of `vecF_g` is shown as `vecF_(g _|_)`. This force, `vecF_(g _|_)`, is equal and opposite to the vertical component force, `vecF_N`, of the road pushing up on the car's tires.
Both the component of force due to gravity pulling down the incline and the component force due to centripetal acceleration of the car through the turn must be offset by frictional force (provided by the tires) to keep the car from accelerating either up or down the incline.
The sum of the offsetting forces, the frictional force `vecF_f`, is toward the direction of center of the turn and parallel to the banked surface when the force component of the centripetal force parallel to the inclined plane is greater than the parallel force due to gravity, `vecF_("g ||")`, and keeps the car from sliding outward during the turn.
If the car is moving slow enough, the frictional force, `vecF_f`, is up the incline since the car's centripetal force can be less than the gravitational force pulling the car down the incline.
`F_N` can be determined by assuming the car stays on the road surface and all the forces perpendicular to the road sum to zero:
Eq. 1: `sum vecF_(_|_) = vecF_N + vecF_(g _|_) = vecF_N + vecF_g * cos(phi) = vecF_N - m*vecg cos(phi) = 0`
So it follows that:
Eq. 2: `|vecF_N| = m*g cos(phi)`
Since the gravitational force pulling down the incline is:
Eq. 3: `vecF_"g ||" = vecF_g * sin(phi)`
Then the opposing frictional force is:
Eq. 4: `|vecF_"fg"| = -|vecF_"g ||" | = -|vecF_g| * sin(phi) = m*vecg*sin(phi)`
The centripetal force is given by:
Eq. 5: `|vecF_c| = m * v^2 / r`
And from the centripetal force the opposing frictional force component can be derived:
Eq. 6: `|vecF_"fc"| = -|vecF_c| * cos(phi) = (-m * v^2 / r ) * cos(phi)`
With both forces of friction, `F_"fg"` and `F_"fc"`, the frictional force, `F_f` can be determined:
Eq. 7: `|vecF_f| = |vecF_"fg" | + |vecF_"fc" | = m*g*sin(phi) - (m * v^2 / r ) * cos(phi)`
This magnitude of the frictional force, `|vecF-f|`, is the instantaneous value of the force required to keep the car moving smoothly through the banked curve. There are two cases to consider here:
- If the frictional force, `|vecF-f|`, is positive, the car is moving slow enough that the force of gravity outweighs the centripetal force. If the coefficient of static friction is not sufficient, which would likely only be if the track were wet or slippery due to some spill, the car would slide down the ramp as it traveled through the curve.
- If the frictional force, `|vecF-f|`, is negative, the car's centripetal force outweighs the gravitational force. If the coefficient of static friction is not sufficient to create enough friction, the car would slide upward in the turn.
Usage
Only the effect of Earth Gravity is considered a the component force pulling the vehicle down the incline in this equation.